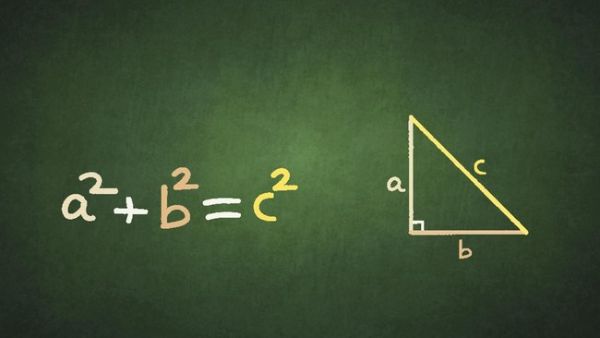Rumus Phytagoras adalah persamaan yang digunakan untuk menghitung salah satu sisi dari bangun segitiga yang memiliki sudut siku-siku. Selain objek yang memang berbentuk segitiga, rumus ini juga bisa digunakan untuk menghitung sisi bangun lainnya yang dimisalkan berbentuk segitiga.
Teorema Phytagoras sendiri diambil dari nama filsuf asal Yunani Kuno yakni Phytagoras yang mengembangkan konsep persamaan sisi segitiga siku-siku. Dari teorema ini bisa dihitung berapakah panjang sisi dari segitiga siku-siku yang hanya diketahui panjang dua sisi lainnya.
Mengenal Pengertian Rumus Phytagoras
Phytagoras adalah konsep di dalam dunia Matematika yang digunakan untuk menunjukkan adanya hubungan antara ketiga sisi dari segitiga siku-siku. Nama Phytagoras sendiri diambil dari nama seorang ilmuwan dan filsuf Yunani Kuno yang hidup pada abad 6 SM.
Meski nama teorema matematika ini diambil dari filsuf Yunani Kuno, namun hal yang berkaitan dengan teorema Phytagoras ternyata sudah diketahui jauh sebelumnya oleh bangsa Babilonia dan Cina. Saat itu mereka menyadari bahwa bilangan 3, 4 dan 5 dapat membentuk bangun segitiga siku-siku.
Terlepas dari siapakah orang yang pertama kali mencetuskan konsep mengenai segitiga siku-siku Phytagoras, teorema ini sangat berguna untuk berbagai bidang kehidupan hari ini. Teorema Phytagoras meliputi ketiga sisi segitiga siku-siku dengan dua sisi saling tegak lurus dan satu sisi miring paling panjang.
Sisi miring disebut juga sebagai hipotenusa terletak tepat di depan sudut siku-siku sebesar 90 derajat. Persamaan Phytagoras sangat berguna untuk menghitung panjang salah satu sisi segitiga siku-siku yang tidak diketahui.
Bunyi Teorema dan Rumus Phytagoras
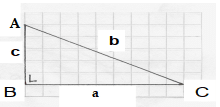
Bunyi dari teorema Phytagoras yakni kuadrat dari sisi miring atau hipotenusa segitiga siku-siku sama dengan kuadrat dari masing-masing sisi tegak yang dijumlahkan. Untuk memudahkan pemahaman mengenai teorema Phytagoras bisa dilihat dari gambar segitiga siku-siku ABC berikut ini.
Pada segitiga siku-siku di atas diketahui bahwa sisi AC merupakan sisi hipotenusa atau sisi miring, Sementara sisi AB dan sisi BC adalah sisi tegak segitiga siku-siku. Berdasarkan konsep Phytagoras maka kuadrat dari AC sama dengan kuadrat dari BC dan AB yang dijumlahkan.
Berikut adalah rumus Phytagoras sisi miring dari bangun segitiga siku-siku ABC di atas:
Persamaan Phytagoras di atas dapat diturunkan untuk menghitung panjang sisi tegak segitiga siku-siku. BC dan AB. Berikut adalah rumus untuk menghitung panjang sisi tegak BC:
BC² = AC² – AB²
Berikut adalah rumus untuk menghitung panjang sisi tegak AB:
AB ² = AC² – BC²
Mengenal Konsep Triple Phytagoras
Di dalam rumus Phytagoras dikenal suatu konsep yang disebut dengan triple phytagoras. Konsep ini digunakan untuk menyebut pasangan bilangan yang dapat memenuhi rumus Phytagoras.
Tiga bilangan bulat yang sudah dikenal terdiri dari bilangan a, b dan c dengan c sebagai hipotenusa atau sisi miring dapat memenuhi persamaan Phytagoras. Ada setidaknya 4 pasangan bilangan yang sudah banyak dikenal memenuhi hukum Triple Phytagoras yakni
- Pasangan bilangan 3, 4, 5
- Pasangan bilangan 5, 12, 13
- Pasangan bilangan 7, 24, 25
- Pasangan bilangan 6, 8, 10
Selain empat pasang bilangan triple Phytagoras di atas, masih ada beberapa pasang bilangan yang juga memenuhi triple Phytagoras sebagai berikut:
- Pasangan bilangan 9, 40, 41
- Pasangan bilangan 8, 15, 17
Untuk menghitung apakah pasangan bilangan memenuhi teorema Triple Phytagoras atau tidak maka cara membuktikannya cukup mudah yakni cukup menggunakan persamaan Phytagoras. Ambil angka terbesar sebagai hipotenusa atau sisi miring dan bilangan lain merupakan panjang sisi tegak segitiga.
Dari sekian banyak pasangan bilangan yang memenuhi konsep tripel Phytagoras, pasangan bilangan 3, 4, 5 adalah bilangan tripel Phytagoras yang paling terkenal. Bahkan pasangan bilangan ini yang banyak digunakan oleh para tukang bangunan untuk membuat pondasi rumah.
Persamaan Phytagoras dalam Identitas Trigonometri
Identitas trigonometri merupakan materi yang menunjukkan adanya relasi antara fungsi trigonometri yang satu dengan fungsi trigonometri lainnya. Dalam menyusun identitas trigonometri maka digunakan teorema Phytagoras sebagai dasar penyusunannya.
Rumus Phytagoras trigonometri digunakan untuk menghitung nilai sinus (sin), cosinus (cos) dan tangen (tan). Nilai sinus, cosinus dan tangen dihitung berdasarkan data kedua sisi tegak segitiga dan sisi miring. Berikut perhitungan trigonometri dasar:
sinus A = sisi di depan sudut A/sisi miring
cosinus A = sisi di samping sudut A/sisi miring
tangen A = sisi di depan sudut A/sisi di samping sudut A
Contoh Soal Materi Phytagoras
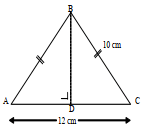
1. Sebuah segitiga sama kaki ABC memiliki panjang kaki-kaki segitiga sebesar 10 cm. Sementara panjang alas segitiga sama kaki sebesar 12 cm. Hitunglah berapa tinggi segitiga sama kaki menggunakan persamaan teorema Phytagoras.
Diketahui:
Sisi BC = 10 cm
Sisi AC (alas) = 12 cm
Ditanya; Tinggi segitiga siku-siku?
Jawab:
Teorema Phytagoras tidak hanya bisa digunakan untuk menghitung sisi segitiga siku-siku namun juga untuk menghitung sisi dari bangun datar lainnya yang memiliki sudut siku-siku.
Bangun ABC merupakan segitiga sama kaki sehingga untuk menghitung tinggi segitiga adalah dengan membagi segitiga menjadi dua sama besar. Tinggi segitiga sama kaki juga membagi alas segitiga ABC sama besar.
Segitiga ABC membentuk dua segitiga siku-siku ADB dan CDB yang sama besar. Untuk menghitung tinggi segitiga siku-siku ACB menggunakan rumus Phytagoras mencari tinggi berikut.
BD² = AB² – AD²
BD² = 10² – 6²
BD² = 100 – 36
BD = √64 = 8 cm
Maka tinggi bangun segitiga sama kaki ABC sebesar 8 cm.
2. Diketahui sebuah segitiga siku-siku FGH mempunyai titik sudut siku-siku di G. Sementara panjang sisi tegak lurus FG sebesar 14 cm dan panjang sisi tegak lurus GH sebesar 48 cm. Tentukan berapakah sisi miring FH menggunakan persamaan Phytagoras.
Diketahui:
Sisi FG = 14 cm
Sisi GH = 48 cm
Ditanya; Sisi miring FH?
Jawab:
Untuk menghitung panjang sisi miring FH menggunakan persamaan Phytagoras sebagai berikut:
FH² = FG² + GH²
FH² = 14² + 48²
FH² = 196 + 2304
FH² = 2500
FH = √2500
FH = 50 cm
Maka panjang sisi miring segitiga siku-siku sebesar 50 cm
3. Sebuah bangun persegi panjang memiliki panjang 25 cm dan lebar 12 cm. Hitunglah berapa panjang diagonal dari bangun persegi panjang tersebut.
Diketahui:
p = 25 cm
l = 12 cm
Ditanya: Panjang diagonal persegi panjang
Jawab:
Untuk menghitung panjang diagonal persegi panjang bisa digunakan rumus Phytagoras dengan menjadikan diagonal persegi panjang sebagai sisi miring segitiga siku-siku.
d² = p² + l²
d² = 25² + 12²
d² = 625 + 144
d² = 769
d = 27,73 cm
Rumus Phytagoras memiliki manfaat yang sangat luas tidak hanya untuk menghitung panjang salah satu sisi bangun segitiga saja namun juga aplikasi lain seperti jarak gerak benda dalam Fisika dan sebagainya. Beberapa pasang bilangan bulat disebut triple Phytagoras karena memenuhi persamaan Phytagoras.
Baca Juga: