Tsunami diketahui sebagai bencana alam yang sering terjadi di Indonesia. Tsunami dapat memberikan dampak buruk bagi makhluk hidup bahkan merusak lingkungan. Anda perlu mengetahui proses terjadinya tsunami untuk lebih memahami tsunami.
Tsunami sendiri harus dipelajari karena ada beberapa faktor yang menjadi penyebabnya. Selain itu, dengan mempelajari tsunami, Anda bisa mengetahui dampak apa yang ditimbulkan dari tsunami sehingga bisa mewaspadainya dengan baik.
Apa Itu Tsunami?
Jika dilihat secara bahasa kata dari Tsunami ini berasal dari “Tsu” yang artinya pelabuhan dan “Nami” adalah gelombang. Jadi, dapat disebutkan bahwa tsunami adalah gelombang laut yang biasanya menerjang pelabuhan.
Sedangkan secara istilah, pengertian tsunami sudah dijelaskan oleh website dari ESDM yang menyebut bahwa tsunami merupakan gelombang laut yang menjalar dengan cepat yaitu sampai lebih dari 900km per jamnya.
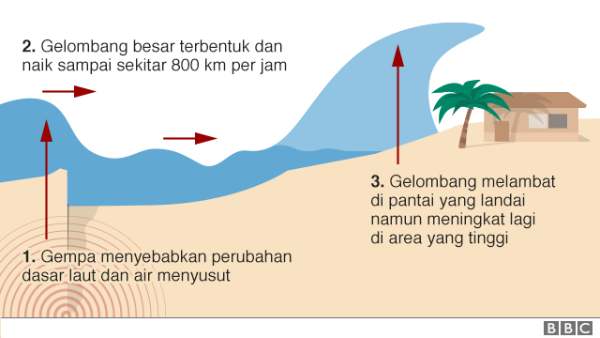
Penyebab dari tsunami ini terjadi karena gempa bumi yang ada di dasar laut sehingga air laut tersebut menimbulkan gelombang yang besar dan akhirnya menghantam daerah pesisir sampai dengan pemukiman warga.
Proses Terjadinya Tsunami
Ada beberapa proses terjadinya tsunami yang disebabkan oleh beberapa faktor tidak hanya dari gempa bumi, tetapi juga karena faktor lainnya. Untuk mengetahuinya lebih detail terkait terjadinya tsunami simak informasinya berikut.
1. Karena Gempa Bumi
Proses yang pertama disebabkan karena gempa bumi yang ada di dasar laut. Meskipun begitu, tidak semua gempa di laut bisa menyebabkan tsunami. Hal ini tergantung dari kekuatan gempanya. Umumnya yang memiliki kekuatan di atas 7 skala magnitudo yang dapat menghasilkan gempa bumi besar.
Jika kekuatan gempanya semakin besar, maka tsunami yang terjadi juga semakin besar dan memiliki dampak yang berbahaya. Contohnya gempa bumi besar di Aceh yang menyebabkan peristiwa tsunami yang berbahaya.
Pada saat itu, kekuatan gempa yang melanda mencapai 9,1 skala magnitudo sehingga tsunami yang dihasilkan juga semakin besar.
2. Karena Tanah Longsor
Proses terjadinya tsunami berikutnya adalah karena tanah longsor. Tsunami dapat terjadi ketika ada tanah longsor baik yang terjadi di laut maupun daratan. Contohnya adalah longsoran es dan batuan yang akhirnya jatuh ke Teluk Lituya di Alaska.
Dari peristiwa ini akhirnya membuat tsunami akibat kekuatan tanah longsornya yang membuat gelombang air laut besar. Pada saat itu, tinggi gelombangnya mencapai 350 sampai dengan 500 meter yang akhirnya menghancurkan berbagai pohon dan semak-semak.
Tidak hanya itu, ada dua korban tewas yang merupakan pemancing pada saat peristiwa tersebut. Selain itu, tanah longsor di bawah laut bisa terjadi karena adanya gempa. Oleh sebab itu, tanah longsor yang terjadi bisa memperparah kondisi tsunami karena gempa.
Bahkan, fenomena tersebut bisa menyebabkan tsunami dengan kekuatan yang lebih besar sehingga memiliki risiko yang lebih berbahaya.
3. Karena Aktivitas Vulkanik
Selain dari penyebab yang sudah disebutkan di atas, aktivitas vulkanik juga menjadi salah satu faktor penyebab terjadinya tsunami. Aktivitas vulkanik terutama apabila gunung berapinya dekat dengan laut maka risiko terkena tsunami juga semakin besar.
Hal ini menyebabkan naik atau turunnya bibir gunung tersebut sehingga dapat menimbulkan tsunami. Hal ini juga sama dengan tsunami akibat gempa bumi. Selain itu, prosesnya dapat terjadi karena letusan besar gunung yang akhirnya akan menghancurkan pulau gunung tersebut di tengah laut.
Oleh sebab itu, air yang ada disekelilingnya akan bergerak dan bergejolak akibat guncangan tersebut sehingga menimbulkan gelombang besar. Contoh tsunami akibat letusan gunung berapi yaitu terjadi di tahun 1883.
Pada saat itu, terjadi letusan gunung Krakatau yang menyebabkan timbulnya bencana alam susulan yaitu tsunami dengan tinggi gelombang lebih dari 40 m. Dari dampak tsunami ini membuat 5000 kapal menjadi hancur serta banyak pulau kecil disekitarnya yang tenggelam.
Selain itu, letusan tersebut menyebabkan 36.0000 orang tewas.
4. Kecepatan Gelombang Laut
Penting diketahui proses terjadinya tsunami ini juga bergantung pada kecepatan gelombang. Sedangkan kecepatan gelombang laut dipengaruhi oleh kedalaman. Contohnya ketika laut punya kedalaman sekitar 7 ribu meter, kecepatannya bisa mencapai 942,9 km/jam.
Kecepatan ini tentu sangat cepat seperti pesawat jet. Namun, tinggi gelombang ketika ada di tengah umumnya tidak tinggi dan hanya mencapai 60 cm. Itulah sebabnya jika kapal yang ada di tengah laut tidak merasakan tsunami meskipun nyatanya di pesisir gelombang lautnya besar.
Langkah Penyelamatan dari Tsunami
Ada beberapa tips mitigasi bencana tsunami yang perlu Anda lakukan. Tujuannya agar dapat menyelamatkan diri ketika bencana ini melanda. Langkah-langkahnya adalah sebagai berikut:
- Apabila ada guncangan gempa bumi yang dirasakan di sekitar pantai serta pantai surut tiba-tiba, Anda perlu berlari ke daerah yang tinggi. Contohnya seperti perbukitan atau bangunan yang tinggi.
- Dilarang mendekat ke area pantai apabila mendengar berita tentang tsunami di wilayah Anda. Jika ada di kapal, segera arahkan perahu ke laut.
- Apabila gelombang tsunami pertama datang dan surut, Anda tidak boleh langsung turun ke dataran rendah. Dikhawatirkan akan ada gelombang lain yang menerjang.
- Selanjutnya, berikan pertolongan pertama untuk korban apabila tsunami sudah benar-benar tidak melanda daerah tersebut.
Jenis-jenis Tsunami
Ada beberapa jenis tsunami berdasarkan UNESCO yang dilihat berdasarkan waktu terjadinya, yaitu sebagai berikut:
1. Tsunami Lokal
Disebut sebagai tsunami lokal kerana jarak tsunami ke daratan relatif dekat sehingga dampak yang dirasakan setelah tsunami terjadi sekitar 1 jam. Umumnya dampaknya hanya sekitar 100 km dari daratan.
2. Tsunami Regional
Untuk jenis tsunami regional yaitu tsunami yang terjadi sekitar 100 sampai 1000 km dari daratan. Jenis ini membutuhkan waktu sekitar 1 sampai 3 jam untuk mencapai daratan. Jadi, masyarakatnya memiliki cukup waktu untuk menyelematkan diri.
3. Tsunami Jarak Jauh
Jenis tsunami jarak jauh atau tsunami samudera adalah tsunami dengan dampak yang luas dan berbahaya. Tsunami ini tergolong berbahaya meskipun jaraknya jauh dari daatan yaitu sekitar 1000 km. Sehingga membutuhkan waktu sampai 3 jam untuk mencapai daratan.
Tsunami ini memungkinkan penduduk pantai dapat menyelematkan diri lebih mudah karena jarak waktunya yag masih lama. Namun, jika sudah mencapai daratan, maka dampaknya cukup besar dan meliputi wilayah luas.
4. Tsunami Meteorologi
Tsunami ini terjadi mirip dengan bencana alam tersebut, tetapi disebabkan oleh gangguan di atmosfer seperti badai, angin topan, gelombang gravitasi di lapisan udara, dsb. Dampak yang ditimbulkan juga mirip dengan tsunami pada umumnya karena bisa merusak kawasan pesisir.
5. Microtsunami
Jenis tsunami yang terakhir adalah microtsunami. Sesuai dengan namanya, jenis tsunami ini memiliki gelombang yang kecil sehingga sulit terlihat secara kasat mata. Untuk mendeteksinya diperlukan alat khusus.
Meski sulit terdeteksi, tsunami ini dinilai berbahaya karena sulit diprediksi datangnya.
Proses terjadinya tsunami bisa disebabkan oleh beberapa faktor mulai dari gempa bumi, tanah longsor, aktivitas vulkanik, sampai dipengaruhi juga oleh kecepatan gelombangnya. Selain itu, Anda perlu memperhatikan cara untuk menyelematkan diri dari bencana tsunami ini.
Baca Juga: